* 경사하강법(Gradient descent)
함수의 기울기를 따라 아래로 이동하면서 손실함수의 값을 최소화하는 최적화 알고리즘이다.
이름 그대로 gradient = 기울기(경사), descent(하강) 즉, ‘기울기를 하강한다’는 의미를 담고 있다.
손실함수란 예측값과 실제값(y)의 차이인 오차를 비교하는 함수이다.

위 그림처럼, 손실함수는 2차 함수 그래프 형태를 가진다.
최적화는 이 손실함수가 최솟값인 알파를 찾아 나가는 과정을 말한다.
* 경사하강법을 통한 최적화 과정
1. 초기 파라미터 설정
파라미터를 임의의 값으로 초기화한다. 선형회귀의 경우 계수와 절편으로 임의의 값을 설정한다.
2. 손실 함수 계산
현재 지점의 기울기를 계산하고, 파라미터 조정 방향을 결정한다. 손실함수의 기울기가 음수이면 계수를 증가시키고 양수이면 감소시켜서 손실을 줄인다.
3. 파라미터 업데이트
계산된 기울기를 사용하여 파라미터를 업데이트한다. 손실함수를 최소화하기 위해 파라미터를 조금씩 조 정하면서 최적값을 찾아간다. 이때 학습률이 사용되는데, 학습률은 업데이트 한번 당 파라미터를 얼마나 조정할지 결정한다.
4. 최적값을 찾을 때까지 이 과정을 반복한다.
만약 학습률이 너무 크면 발산할 가능성이 높고, 학습률이 너무 작을 경우 수렵이 늦어질 수도 있기 때문에 적절한 학습률을 찾는 것이 중요하다.
* 문제

주어진 자동차의 마력과 연비 데이터를 통해 선형 회귀 모델을 학습하고, 경사하강법을 사용하여 최적의 모델 파라미터(계수와 절편)를 찾아라.
* 코드
1. 라이브러리 임포트
import pandas as pd # 판다스 임포트
import numpy as np # 넘파이 임포트
import matplotlib.pyplot as plt # 맷플롯립 임포트
데이터프레임 생성을 위한 판다스, 배열을 다루기 위한 넘파이, 그래프 출력을 위한 맷플롯립 라이 브러리를 임포트 하였다.
2. 데이터 준비
# 데이터 준비
df = pd.DataFrame({ # 데이터 프레임을 생성하여 변수 df에 할당
'name': ['A', 'B', 'C', 'D', 'E', 'F', 'G'], # 자동차 이름
'horse_power': [130, 250, 190, 300, 210, 220, 170], # 마력
'efficiency': [16.3, 10.2, 11.1, 7.1, 12.1, 13.2, 14.2] # 연비
})
pd.DataFrame() 함수로 자동차의 이름, 마력, 연비 데이터를 구조화하여 준비하였다.
데이터프레임은 행과 열로 구성된 테이블 형식의 자료구조로, 표를 출력할 때만 필요한 작업이 아니라, 데이 터를 효율적으로 다루기 위해 많이 사용한다.
3. 선형 회귀 모델 학습 준비, 넘파이 배열로 변환
# 선형 회귀 모델 학습 준비, 넘파이 배열로 변환
X = df['horse_power'].values # 마력 데이터값을 X에 할당
y = df['efficiency'].values # 연비 데이터값을 y에 할당
‘horse_power’ 마력 데이터와 ‘efficiency’ 연비 데이터를 넘파이 배열로 변환하여 각 x, y에 할당하였다. 이렇게 준비된 x는 독립변수, y는 종속변수가 된다.
넘파이 배열로 변환하는 이유는 선형 회귀 모델을 학습하고 예측하는 데 사용하기 위함이다. 선형 회귀 모델 은 독립변수와 종속변수 간의 관계를 모델링하는데, 이 변수들은 일반적으로 넘파이 배열 형태로 사용된다.
4. 초기 파라미터, 학습률, 반복 횟수 설정
# 초기 파라미터 설정
param = np.array([-1.0, 1.0]) # 계수와 절편
# 학습률과 반복 횟수 조정
learning_rate = 0.000002 # 학습률
learning_iteration = 100000000 # 반복 횟수
경사하강법에서는 초기 파라미터를 임의의 값으로 설정하는데, 선형회귀의 경우 계수와 절편으로 설정한다.
경사하강법에서 사용되는 학습률과 반복 횟수를 각 0.000002, 100000000로 설정하였다.
여러 가지 값들을 시도해 보고, 최적의 조합을 찾아낸 값이다.
5. 경사하강법
for i in range(learning_iteration): # 100000000번 반복하며
prediction = param[0] * X + param[1] # 예측값 계산
error = prediction - y # 오차 계산
param[0] -= learning_rate * np.dot(error, X) / len(X) # 계수 조정
param[1] -= learning_rate * np.sum(error) / len(X) # 절편 조정
먼저, 초기 파라미터를 사용하여 독립변수(마력)에 대해 모델이 예측하는 종속변수(연비)에 대한 예측값을 계산한다.(계수 * X + 절편)
계산된 예측값에서 실제값 y를 빼서 오차를 계산한다.
오차 확인 후, 손실함수(예측값과 실제값의 차이)를 최소화하기 위해 계수와 절편을 조정한다.
손실함수의 기울기가 음수이면 계수를 증가시키고 양수이면 감소시켜서 손실을 줄인다.
# 10000000 번 반복마다 중간결과 출력
if i % 10000000 == 0:
# 반복 횟수, 게수, 절편 출력
print(f"반복 횟수 {i}: 계수 = {param[0]}, 절편 = {param[1]}")
df.plot(kind='scatter', x='horse_power', y='efficiency')
# 그래프 출력
plt.plot([min(X), max(X)], [h(min(X), param), h(max(X), param)])
중간결과를 보기 위해, 10000000번 반복마다 반복 횟수, 계수, 절편과 함께 그래프를 출력하도록 하였다.
6. 최종 결과 출력
# 최종 결과 출력
print('계수:', param[0])
print('절편:', param[1])
predicted_efficiency = param[0] * 270 + param[1]
print('270 마력 자동차의 예상 연비:', round(predicted_efficiency, 2), 'km/l')
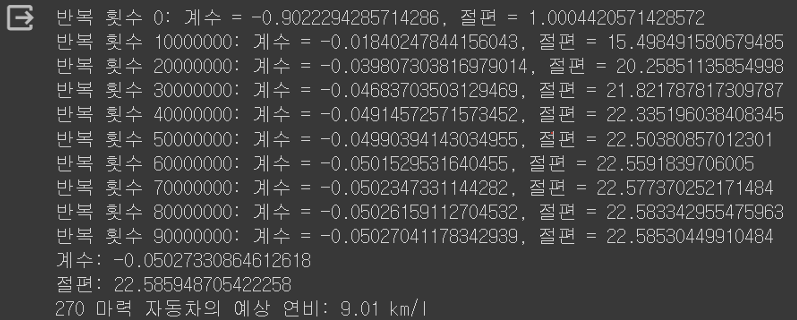


그래프 출력 결과, 점들이 점점 직선에 수렴하는 것을 볼 수 있다.
끝.
'전공 수업 > 머신러닝' 카테고리의 다른 글
| 젯슨나노 부팅 오류 (0) | 2024.07.31 |
|---|---|
| [머신러닝] 결정 트리(와인 분류) (0) | 2023.02.21 |
| [머신러닝] 확률적 경사 하강법 (0) | 2023.02.18 |
| [머신러닝] 로지스틱 회귀(생선 확률 예측) (0) | 2023.02.10 |
| [머신러닝] 릿지, 라쏘(농어 무게 예측3) (0) | 2023.01.31 |